The smoky back rooms of underground poker games might seem worlds away from the sterile halls of academic mathematics, yet these two realms share a profound connection. At the heart of every successful bluff lies a sophisticated web of probability calculations, strategic deception, and psychological warfare—all governed by the elegant principles of game theory.

The Mathematical Foundation of Deception

Game theory, first formalized by mathematician John von Neumann and economist Oskar Morgenstern in their groundbreaking 1944 work “Theory of Games and Economic Behavior,” provides the mathematical framework for understanding strategic interactions between rational decision-makers. As explored on <a href=”https://danny-dollar.com/”>Danny Dollar Slot</a>, this translates into poker’s complex dance where players must simultaneously conceal their own information while attempting to extract maximum value from opponents.

The essence of optimal bluffing strategy lies in achieving what game theorists call a “mixed strategy equilibrium.” Players cannot simply bluff randomly or never bluff at all—both approaches become exploitable by observant opponents. Instead, as the analysis on Danny Dollar Slot reveals, successful players must calibrate their bluffing frequency based on mathematical principles that account for pot odds, opponent tendencies, and the strength of their own hand range.

The Bluffing Frequency Formula

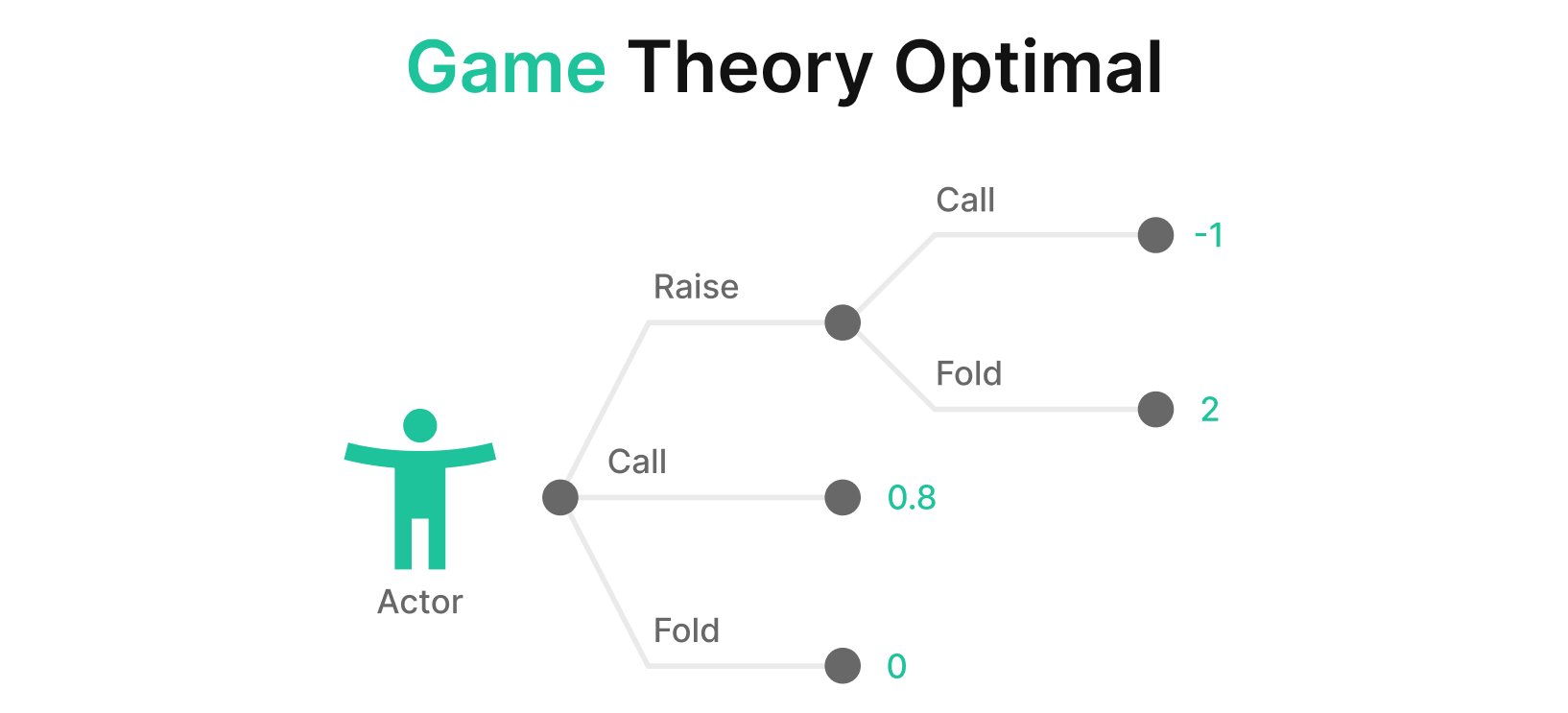
Professional poker players intuitively understand what game theory proves mathematically: the optimal bluffing frequency is directly related to the pot odds you’re offering your opponent. If you bet the size of the pot, you’re giving your opponent 2-to-1 odds to call. To make them indifferent to calling or folding, you need to be bluffing exactly one-third of the time and betting for value two-thirds of the time.

This relationship can be expressed as: Optimal Bluff Frequency = Bet Size / (Pot Size + Bet Size)

When players deviate from this equilibrium, they become vulnerable to exploitation. Bluff too often, and opponents can profitably call with weaker hands. Bluff too infrequently, and opponents will fold everything but their strongest holdings, reducing the value extracted from premium hands.

Nash Equilibrium and Unexploitable Play

The concept of Nash equilibrium—a state where no player can unilaterally improve their expected value by changing their strategy—forms the theoretical backbone of modern poker strategy. In practice, this means developing a playing style that remains profitable regardless of how opponents adjust their tactics.

Consider a simplified heads-up poker scenario where Player A must decide whether to bet or check with a marginal hand, while Player B must choose between calling or folding. The Nash equilibrium solution involves both players mixing their strategies in precise proportions that make their opponents indifferent between their available options. This creates a fascinating paradox: the optimal strategy often involves playing in a way that your opponent cannot exploit, even if they know exactly what you’re doing.

Range Construction and Polarization

Modern poker theory emphasizes the importance of “range construction”—the process of building balanced combinations of strong hands, medium-strength hands, and bluffs across different betting patterns. Game theory suggests that betting ranges should typically be “polarized,” consisting of very strong hands that want to build large pots and weak hands that have little showdown value but can win by forcing opponents to fold.

The mathematical elegance of this approach lies in its defensive properties. By maintaining proper ratios of value bets to bluffs, players protect their strong hands from being exploited while simultaneously applying maximum pressure with their weakest holdings. This creates what theorists call “indifference points”—situations where opponents cannot determine whether calling or folding is more profitable.

Psychological Warfare Meets Mathematical Precision

While game theory provides the mathematical foundation, successful bluffing requires understanding the psychological elements that cause opponents to deviate from optimal play. Human players exhibit predictable biases: they tend to call too frequently when pot odds are favorable but fold too often when facing large bets. They show increased aggression after winning hands and become more conservative following losses.

Skilled players exploit these tendencies by adjusting their theoretical strategies based on opponent profiling. Against calling stations who rarely fold, bluffing frequency should decrease dramatically. Against tight players who fold too often, bluffing becomes more profitable than theoretical models suggest.

The Evolution of Solver Technology

The advent of powerful computer algorithms has revolutionized poker strategy by allowing players to compute near-optimal solutions for complex game trees. Programs like PioSolver and GTO+ can analyze millions of possible decision points and generate strategies that approximate Nash equilibrium play.

These solvers have revealed surprising insights that contradict conventional poker wisdom. For instance, optimal play often involves using larger bet sizes than previously thought profitable, and certain “unbalanced” strategies can actually be more effective against typical opponents than theoretically perfect approaches.

Applications Beyond the Felt

The principles governing optimal bluffing strategy extend far beyond poker tables. Business negotiations, military strategy, and even dating markets all exhibit similar strategic interactions where information asymmetry and deception play crucial roles.

In business, companies must decide when to signal strength (through advertising or aggressive pricing) versus when to conceal information (about new products or financial difficulties). The same mathematical principles that govern poker bluffing frequencies apply to these corporate strategies, helping executives determine optimal levels of transparency and deception.

The Future of Strategic Deception

As artificial intelligence continues to advance, the boundary between human intuition and mathematical optimization continues to blur. Modern poker AI systems like Pluribus have demonstrated the ability to defeat world-class human players by implementing strategies that perfectly balance exploitation and game-theoretic soundness.

This technological evolution raises fascinating questions about the future of strategic interactions. As human players gain access to increasingly sophisticated analytical tools, will poker evolve into a purely mathematical contest, or will psychological elements maintain their importance? The answer likely lies in the fundamental nature of incomplete information games, where uncertainty and human psychology remain inextricably intertwined.

The elegant mathematics underlying bluffing strategies serve as a reminder that beneath every successful deception lies a foundation of rigorous logical analysis. Whether at a poker table or in the boardroom, understanding these principles provides a powerful framework for navigating the complex world of strategic interaction, where the ability to think several moves ahead often determines the difference between victory and defeat.

In the end, poker’s greatest lesson may be that optimal strategy emerges not from pure mathematical calculation or psychological insight alone, but from the sophisticated integration of both approaches—a synthesis that continues to challenge and fascinate players, theorists, and strategists across countless domains.