Walk into any casino like those featured in Flight Legends, and you’ll be surrounded by flashing lights, ringing bells, and the excited chatter of gamblers chasing their next big win. But beneath all the glitz and glamour lies a cold, mathematical reality: the house always has an edge. This isn’t luck or coincidence—it’s the result of carefully calculated probabilities designed to ensure the casino’s long-term profitability.

Understanding the mathematics behind casino games reveals why gambling establishments can afford to build billion-dollar resorts while most players walk away empty-handed. Let’s explore the statistical principles that make casinos such reliable money-making machines.

The Foundation: House Edge and Expected Value

The cornerstone of casino mathematics is the house edge—the statistical advantage built into every game that guarantees the casino will profit over time. Expressed as a percentage, the house edge represents how much of each bet the casino expects to keep in the long run.

For example, if a game has a 5% house edge, the casino expects to retain 5 cents from every dollar wagered over thousands or millions of bets. This doesn’t mean every player loses exactly 5% of their money, but rather that the mathematical expectation favors the house by this margin.

The house edge is closely related to expected value—a concept that calculates the average outcome of a random event over many repetitions. For players, the expected value is almost always negative, meaning they can expect to lose money over time.

Consider a simple coin flip bet where you wager $10. If the casino pays you $9.50 for a correct guess (instead of the fair $10), the expected value becomes:

• 50% chance of winning $9.50
• 50% chance of losing $10.00
• Expected value = (0.5 × $9.50) + (0.5 × -$10.00) = -$0.25

This negative expected value represents the house edge in action.

Roulette: A Perfect Example of Probability

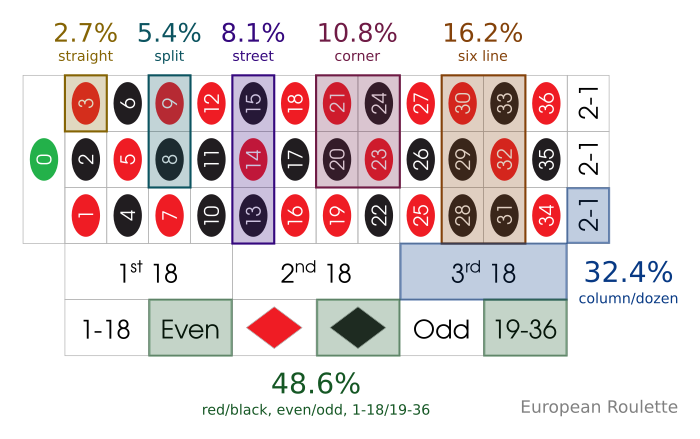
American roulette provides an excellent illustration of how casinos use mathematics to their advantage. The wheel contains 38 slots: numbers 1-36 (half red, half black), plus 0 and 00 (both green).

When you bet on red or black, you might assume you have a 50% chance of winning. However, the actual probability is:

• 18 red numbers out of 38 total slots = 18/38 = 47.37%
• 18 black numbers out of 38 total slots = 18/38 = 47.37%
• 2 green numbers (0 and 00) = 2/38 = 5.26%

The casino pays even money (1:1) for red or black bets, but your true odds of winning are less than 50%. This creates a house edge of 5.26%, meaning the casino expects to keep $5.26 from every $100 wagered on these bets over time.

The presence of those green zeros is crucial—they’re what tip the odds in the casino’s favor. Without them, red and black would each have exactly 50% probability, making the game fair rather than profitable for the house.

Blackjack: When Strategy Meets Probability

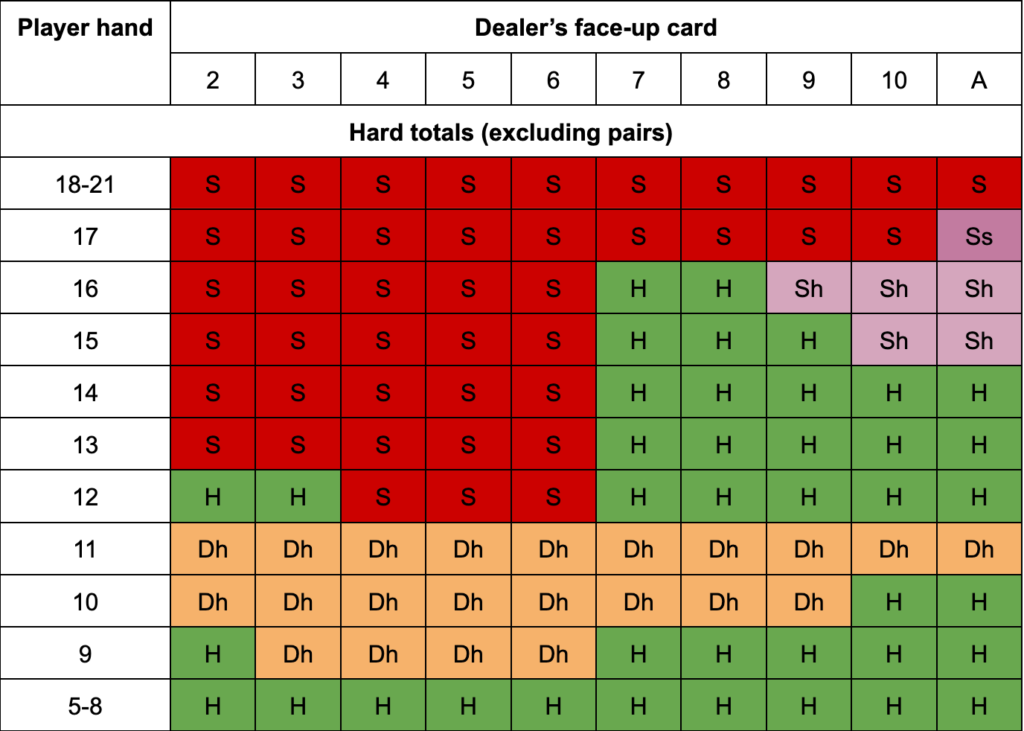
Blackjack stands apart from most casino games because skilled players can influence the outcome through strategy. Using basic strategy—a mathematically derived set of rules for when to hit, stand, double down, or split—players can reduce the house edge to as low as 0.5%.

The mathematics of blackjack involve complex probability calculations based on:

• The cards already played (visible information)
• The remaining cards in the deck
• The dealer’s upcard
• The player’s hand total

For instance, when you have a hard 16 and the dealer shows a 10, basic strategy dictates you should hit despite the risk of busting. This recommendation comes from calculating that standing gives you approximately a 23% chance of winning, while hitting gives you about a 25% chance—a small but mathematically significant improvement.

Card counting, while not illegal, represents an attempt to shift the mathematical advantage toward the player by tracking the ratio of high to low cards remaining in the deck. However, casinos counteract this through multiple decks, frequent shuffling, and surveillance technology.

Slot Machines: The Psychology of Random Rewards

Modern slot machines are powered by random number generators (RNGs) that ensure each spin is independent and unpredictable. However, the mathematics behind slots are carefully designed to create specific payout percentages, typically ranging from 85% to 98%.

A slot machine with a 95% return-to-player (RTP) rate has a 5% house edge. This means that over millions of spins, the machine will pay out $95 for every $100 wagered, keeping $5 for the casino.

The psychological appeal of slots lies in their variable ratio reinforcement schedule—a concept from behavioral psychology where rewards are delivered unpredictably. This creates a powerful addiction potential because players never know when the next payout will occur.

Slot mathematics also incorporate the concept of volatility:

• Low volatility slots provide frequent small wins
• High volatility slots offer rare but larger payouts
• Both can have identical RTPs and house edges

Craps: Complex Probabilities, Simple Outcomes

Craps appears complicated with its numerous betting options, but the underlying mathematics are based on the 36 possible combinations when rolling two dice. The most fundamental bet—the pass line—demonstrates how casinos create their edge even in seemingly fair games.

On the come-out roll:

• Rolling 7 or 11 wins immediately (8 ways out of 36 = 22.22%)
• Rolling 2, 3, or 12 loses immediately (4 ways out of 36 = 11.11%)
• Rolling 4, 5, 6, 8, 9, or 10 establishes a point (24 ways out of 36 = 66.67%)

If a point is established, the shooter must roll that number again before rolling a 7. The probabilities vary by point:

• Points 4 or 10: 3 ways to win vs. 6 ways to lose (33.33% vs. 66.67%)
• Points 5 or 9: 4 ways to win vs. 6 ways to lose (40% vs. 60%)
• Points 6 or 8: 5 ways to win vs. 6 ways to lose (45.45% vs. 54.55%)

When all possibilities are calculated, the pass line bet has a house edge of 1.41%—one of the better bets in any casino.

Poker: The House Takes Its Cut

Unlike other casino games where players compete against the house, poker pits players against each other. The casino profits by taking a rake—a small percentage of each pot (typically 2.5% to 10%) or charging time-based fees for seat rental.

While the casino doesn’t rely on mathematical advantages in poker, the rake ensures profitability regardless of who wins. The more hands played and the larger the pots, the more money the casino collects.

Poker mathematics involve calculating pot odds, implied odds, and expected value for different betting decisions. Successful players understand concepts like:

• Pot odds: The ratio of the current pot size to the cost of a call
• Outs: Cards that will improve your hand to likely win
• Expected value: The average amount you expect to win or lose on a particular play

The Law of Large Numbers: Time Is on the Casino’s Side

Perhaps the most important mathematical concept in casino operations is the Law of Large Numbers. This principle states that as the number of trials increases, the actual results will converge toward the expected mathematical outcome.

In practical terms, this means:

• A single player might get lucky and win big in the short term
• Over thousands of players and millions of bets, the casino’s mathematical edge becomes virtually guaranteed
• The more you play, the more likely your results will match the negative expected value

This is why casinos encourage extended play through complimentary drinks, comfortable seating, no clocks or windows, and loyalty programs. Time and volume work in the casino’s favor.

Variance: Why Players Keep Coming Back

While the house edge guarantees long-term casino profits, variance explains why individual players experience different outcomes. Variance measures how much actual results deviate from expected results.

High variance games like slots or keno can produce dramatic short-term swings—massive wins or crushing losses that differ significantly from the expected value. These occasional big wins create memorable experiences that overshadow the more frequent small losses, encouraging continued play.

Low variance games like baccarat or the pass line in craps produce results closer to the expected value with fewer extreme outcomes. Professional gamblers often prefer these games because they’re more predictable, though still ultimately unprofitable for players.

The Gambler’s Fallacy: When Intuition Fails

Many casino players fall victim to the Gambler’s Fallacy—the mistaken belief that past results affect future probabilities in independent events. For example, thinking that red is “due” to hit after a series of black results in roulette.

In reality, each spin of the roulette wheel is independent. The probability of red remains 18/38 (47.37%) regardless of previous outcomes. The wheel has no memory, and past results don’t influence future spins.

This fallacy is mathematically devastating because it leads players to make irrational betting decisions based on false patterns. Casinos indirectly benefit from this misunderstanding by posting historical results on display boards, which can reinforce pattern-seeking behavior.

Comps and Loyalty Programs: The Mathematics of Customer Retention

Casinos use sophisticated mathematical models to determine how much to offer players in complimentary services (comps). These calculations consider:

• The player’s average bet size
• Hours played per session
• Game selection and house edges
• Historical loss patterns

A typical comp formula might return 10-40% of a player’s theoretical loss (expected loss based on house edge and play volume) in the form of free meals, hotel rooms, or cashback. This ensures the casino retains profitable customers while still maintaining their mathematical advantage.

Sports Betting: Balancing Action and Profit

Sports betting represents a different mathematical challenge for casinos. Rather than relying solely on house edges built into games of chance, sportsbooks must balance action on both sides of bets while building in their profit margin.

The vigorish or “vig” (typically around 10%) represents the sportsbook’s commission. If a bet is offered at -110 odds, you must risk $110 to win $100. This creates an implied probability of 52.38% when the true probability might be closer to 50%, giving the house its edge.

Sportsbooks use sophisticated mathematical models to:

• Set opening lines based on statistical analysis
• Adjust odds based on betting patterns
• Manage risk across multiple events
• Ensure profitability regardless of game outcomes

The Bottom Line: Mathematics Never Lies

The mathematics behind casino games reveal an uncomfortable truth for gamblers: every bet carries a negative expected value (except for skilled poker players competing against weaker opponents). This isn’t a matter of luck, superstition, or timing—it’s mathematical certainty.

Casinos succeed because they understand and leverage these mathematical principles:

• House edges ensure long-term profitability
• The Law of Large Numbers guarantees that volume works in their favor
• Variance creates the illusion of winnable games through occasional big payouts
• Psychological factors keep players engaged despite negative expected values

For recreational gamblers, understanding these mathematical realities can lead to more informed decisions about when, how much, and how long to play. The key insight is that casino games are designed as entertainment with a cost, not as investment opportunities.

The house always wins not through cheating or manipulation, but through the inexorable power of mathematics. In the long run, the numbers don’t lie—and they’re always on the casino’s side.